< The "Conservation of Energy" in Relation Certain Views of the Theosophists (continued from page 7-135) >
weight of a body by its mass. As unit of length for the measurement of height we may take the foot of twelve inches. Our unit of work will thus be the foot-pound, or one pound raised through one foot. And if we designate work by W, mass by m, and height by h, we have the relation:—

Thus, referring to the diagram, let the mass of m be 5 lbs., and let it be raised 5 feet from the surface (S) of the earth. Then the work done in raising it will be
And the same value will express the potential energy stored up in the mass, or its energy of position.
When we carefully consider the meaning of the expression “raising a weight,” we find that it signifies separating two masses, one of which, in the present case, is the earth and the other the mass m. The two masses are in fact pushed apart; and it is indubitable that they are both caused to move, although the motion of the earth is as much smaller than that of m as its mass is larger. We are now enabled to comprehend the following law:—In the separation of masses, work is stored up as potential energy (of position).
Can we not now, from data within our own experience, formulate, at least hypothetically, a proposition applicable to the contrary case? We have all some experience of energy of motion—kinetic energy, or, as it is sometimes called, visible energy. When we have to jump any distance, we generally “take a run” in order to accumulate a little kinetic energy. We cannot well doubt that some kind of energy is stored up in a stone dropped from the top of a house, as well as in one thrown by a boy, in projectiles of a more warlike character, or in a railway train moving at the rate of fifty miles an hour. And, bearing specially in mind the first example, we can readily admit that:—When masses fall together, potential energy becomes converted into kinetic energy.
Now, if we know the number of foot-pounds of work which have been converted into kinetic energy, we shall have no difficulty in expressing the latter in foot-pounds. Thus the mass m (in the diagram), if it be allowed to fall freely through the distance between it and S, will obtain 25 foot-pounds of kinetic energy before it strikes the ground. Presently, we shall imagine what becomes of the kinetic energy when the movement is arrested.
Let us first, however, endeavour to obtain a further insight into the philosophy of motion which has justly been termed the key to nature. Motion is always produced by the action of a force, a term which is correctly applied only to what is familiarly known as a pressure or a pull. The motion of m towards 8 is produced by the pull called gravity. Now gravity is termed an accelerating force; because, when it acts freely upon a mass, it produces uniformly accelerated motion. It is measured by the velocity it communicates to a falling mass, in vacuo, at the end of one second of time, or, what is the same thing, by the velocity it communicates to a mass in any given number of seconds, divided by the number of seconds. Calling velocity, in feet per second v; the number of seconds, t; and the force of gravity, g, we have

since in one second gravity will communicate this velocity to any falling body, if its action be unresisted.
Now, with this datum, by a very simple process of mathematical analysis applied to the factor h in our first formula, we may arrive at several particulars—for instance, the time it would take for m to fall through 5 feet, and the velocity it would obtain at the end of this time; and at one most important generalisation, viz., the measure, in foot-pounds, of the kinetic energy stored up in any moving body. Let us not be afraid of the expression “mathematical analysis,” for this is merely a term expressing an operation which happens to be convenient to us. We already know that energy may be expressed as m x. h; but, unfortunately, in the case of a projectile or a railway train in motion, for instance, we have no means of arriving at h, or the height through which a body would have to fall, under the action of gravity, in order to obtain a given velocity. If, however, the velocity of a falling body were uniform, instead of uniformly accelerated, we should have no difficulty in finding an equation for h. In fact, we all of us know that in the case of uniform velocity of motion, the distance moved through is necessarily as the velocity multiplied into the time of motion. We do not require to be informed that, if a man be walking at the rate of four miles an hour, he will, in three hours, have moved through a distance of three times four, or twelve, miles. In the case of uniform motion the distance moved through would be—
Thus, referring to diagram 2, let the line A B represent a given velocity, and B D a given time during which a body moves uniformly with that velocity, then the distance moved through will be represented by the rectangular A B C D. But suppose the body commences, at the beginning of the
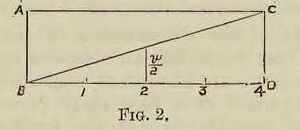
time BD, to move with a uniformly accelerated velocity, until at the end of that time it obtains the velocity C D, what will then be the distance moved through? It is tolerably obvious that in this case we must multiply the mean velocity into time in order to obtain this value. Now the mean velocity will be just half the final velocity, v; so that our formula becomes

In this expression we may substitute for t its value as derived from our second formula. Allow me to assume that no one here has any knowledge of algebra. We at least know that multiplication and division are converse operations; so that if we remove a divisor on one side of an equality, we must insert the same value as a multiplier on the other side, and if we remove a multiplier on one side, we must insert the same value as a divisor on the other. We have thus
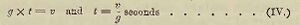


Now this is the equation for kinetic energy, which is well worth any trouble we may have taken to obtain it.
A little algebra may be required to derive from formula Ilia the following expression for the velocity obtained by any body in falling freely through the distance h, viz.:—

Now from this last formula we find that the velocity obtained by the mass m (in diagram 1) in falling freely through 5 feet is

And, from formula Y, the kinetic energy stored up in itwhen it obtains this velocity is
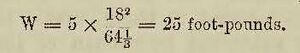
Or the precise value of the work done in raising the mass m through 5 feet.
By formula 1Y, the time taken by m to fall through 5 feet is
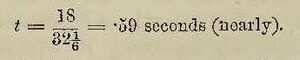
By the formula for kinetic energy, we find that the work stored up in a railway truck weighing 3 tons and moving at the rate of 40 miles an hour is over 160foot tons, and that the projectile of the 100-ton gun, weighing 2,000 lbs., and moving with its initial velocity of 1,493 feet per second, has a kinetic energy of no less than 30,913foot tons. I may here observe that even the latter velocity, and the terrific energy associated with it, sink into insignificance in comparison <... continues on page 7-137 >
Editor's notes
